|
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria (e.g. "two counties over"). In mathematics, a distance function or metric is a generalization of the concept of physical distance. A metric is a function that behaves according to a specific set of rules, and provides a concrete way of describing what it means for elements of some space to be "close to" or "far away from" each other. In most cases, "distance from A to B" is interchangeable with "distance between B and A". See also: Metric (mathematics)
Geometry In neutral geometry, the distance between (x1) and (x2) is the length of the line segment between them: In analytic geometry, the distance between two points of the xy-plane can be found using the distance formula. The distance between (x1, y1) and (x2, y2) is given by: Similarly, given points (x1, y1, z1) and (x2, y2, z2) in three-space, the distance between them is: These formulae are easily derived by constructing a right triangle with a leg on the hypotenuse of another (with the other leg orthogonal to the plane that contains the 1st triangle) and applying the Pythagorean theorem. In the study of complicated geometries, we call this (most common) type of distance Euclidean distance, as it is derived from the Pythagorean theorem, which does not hold in Non-Euclidean geometries. This distance formula can also be expanded into the arc-length formula. In the Euclidean space R, the distance between two points is usually given by the Euclidean distance (2-norm distance). Other distances, based on other norms, are sometimes used instead. For a point (x1, x2, ...,xn) and a point (y1, y2, ...,yn), the Minkowski distance of order p (p-norm distance) is defined as:
p need not be an integer, but it cannot be less than 1, because otherwise the triangle inequality does not hold. The 2-norm distance is the Euclidean distance, a generalization of the Pythagorean theorem to more than two coordinates. It is what would be obtained if the distance between two points were measured with a ruler: the "intuitive" idea of distance. The 1-norm distance is more colourfully called the taxicab norm or Manhattan distance, because it is the distance a car would drive in a city laid out in square blocks (if there are no one-way streets). The infinity norm distance is also called Chebyshev distance. In 2D, it is the minimum number of moves kings require to travel between two squares on a chessboard. The p-norm is rarely used for values of p other than 1, 2, and infinity, but see; super ellipse. In physical space the Euclidean distance is in a way the most natural one, because in this case the length of a rigid body does not change with rotation. The Euclidean distance between two points in space ( Here The Euclidean distance between two objects may also be generalized to the case where the objects are no longer points but are higher-dimensional manifolds, such as space curves, so in addition to talking about distance between two points one can discuss concepts of distance between two strings. Since the new objects that are dealt with are extended objects (not points anymore) additional concepts such as non-extensibility, curvature constraints, and non-local interactions that enforce non-crossing become central to the notion of distance. The distance between the two manifolds is the scalar quantity that results from minimizing the generalized distance functional, which represents a transformation between the two manifolds:
The above double integral is the generalized distance functional between two plymer conformation. s is a spatial parameter and t is pseudo-time. This means that
The algebraic distance is a metric often used in computer vision that can be minimized by least squares estimation. For curves or surfaces given by the equation xCx = 0 (such as a conic in homogeneous coordinates), the algebraic distance from the point x’ to the curve is simply x’Cx’. It may serve as an "initial guess" for geometric distance to refine estimations of the curve by more accurate methods, such as non-linear least squares. In mathematics, in particular geometry, a distance function on a given set M is a function d: M×M → R, where R denotes the set of real numbers, that satisfies the following conditions:
Such a distance function is known as a metric. Together with the set, it makes up a metric space. For example, the usual definition of distance between two real numbers x and y is: d(x,y) = |x − y|. This definition satisfies the three conditions above, and corresponds to the standard topology of the real line. But distance on a given set is a definitional choice. Another possible choice is to define: d(x,y) = 0 if x = y, and 1 otherwise. This also defines a metric, but gives a completely different topology, the "discrete topology"; with this definition numbers cannot be arbitrarily close. Distances between sets and between a point and a set Various distance definitions are possible between objects. For example, between celestial bodies one should not confuse the surface-to-surface distance and the center-to-center distance. If the former is much less than the latter, as for a LEO, the first tends to be quoted (altitude), otherwise, e.g. for the Earth-Moon distance, the latter. There are two common definitions for the distance between two non-empty subsets of a given set:
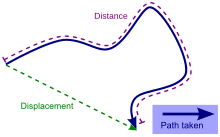
The distance between a point and a set is the infimum of the distances between the point and those in the set. This corresponds to the distance, according to the first-mentioned definition above of the distance between sets, from the set containing only this point to the other set. In terms of this, the definition of the Hausdorff distance can be simplified: it is the larger of two values, one being the supremum, for a point ranging over one set, of the distance between the point and the set, and the other value being likewise defined but with the roles of the two sets swapped. In graph theory the distance between two vertices is the length of the shortest path between those vertices. Distance cannot be negative and distance travelled never decreases. Distance is a scalar quantity or a magnitude, whereas displacement is a vector quantity with both magnitude and direction. The distance covered by a vehicle (for example as recorded by an odometer), person, animal, or object along a curved path from a point A to a point B should be distinguished from the straight line distance from A to B. For example whatever the distance covered during a round trip from A to B and back to A, the displacement is zero as start and end points coincide. In general the straight line distance does not equal distance travelled, except for journeys in a straight line. Directed distances are distances with a direction or sense. They can be determined along straight lines and along curved lines. A directed distance along a straight line from A to B is a vector joining any two points in a n-dimensional Euclidean vector space. A directed distance along a curved line is not a vector and is represented by a segment of that curved line defined by endpoints A and B, with some specific information indicating the sense (or direction) of an ideal or real motion from one endpoint of the segment to the other (see figure). For instance, just labelling the two endpoints as A and B can indicate the sense, if the ordered sequence (A, B) is assumed, which implies that A is the starting point. A displacement (see above) is a special kind of directed distance defined in mechanics. A directed distance is called displacement when it is the distance along a straight line (minimum distance) from A and B, and when A and B are positions occupied by the same particle at two different instants of time. This implies motion of the particle. displace is a vector quantity. Another kind of directed distance is that between two different particles or point masses at a given time. For instance, the distance from the center of gravity of the Earth A and the center of gravity of the Moon B (which does not strictly imply motion from A to B).Shortest path length may be equal to displacement or may not be equal to.Distance from starting point is always equal to magnitude of displacement. For same particle distance travelled is always greater than or equal to magnitude of displacement
Circular distance is the distance traveled by a wheel. The circumference of the wheel is 2π × radius, and assuming the radius to be 1, then each revolution of the wheel is equivalent of the distance 2π radians. In engineering ω = 2πÆ’ is often used, where Æ’ is the frequency.
From Wikipedia, the free encyclopedia : Distance |



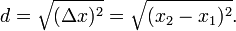

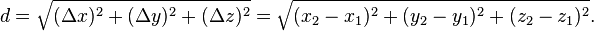


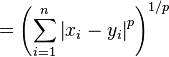


 and
and  ) may be written in a
) may be written in a 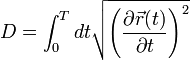
 is the trajectory (path) between the two points. The value of the integral (D) represents the length of this trajectory. The distance is the minimal value of this integral and is obtained when
is the trajectory (path) between the two points. The value of the integral (D) represents the length of this trajectory. The distance is the minimal value of this integral and is obtained when 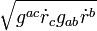 , where
, where 
 is the polymer/string conformation at time
is the polymer/string conformation at time  is the trajectory of an infinitesimal segment of the string during transformation of the entire string from conformation
is the trajectory of an infinitesimal segment of the string during transformation of the entire string from conformation 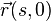 to conformation
to conformation  . The term with cofactor
. The term with cofactor